    ★ 线段 下图中的线段表示小棍，看小棍的摆法多有趣！

（1）一根小棍。可以横着摆，也可以竖着摆。

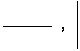
（2）两根小棍。可以都横着摆，也可以都竖着摆，还可以一横一竖摆。

（3）三根小棍。可以像下面这样摆。

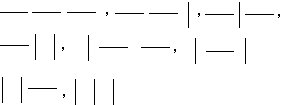
规律分析
 
- 一根小棍有2种摆法，即2^1 = 2种。
- 两根小棍有4种摆法，即2^2 = 4种。
- 三根小棍有8种摆法，即2^3 = 8种。
 
由此可推测规律为：小棍的数量与摆法种数存在指数关系，摆法种数是2的小棍数量次方。
 
公式推导
 
设小棍的数量为n，摆法的种数为S，那么可以得到公式S = 2^n。
 
通过这个公式，我们可以根据小棍的数量n，快速计算出对应的摆法种数S。

可以用数学归纳法来证明公式S = 2^n的正确性，证明过程如下：
 
基础步骤
 
当n = 1时，一根小棍有2种摆法，而2^1 = 2，公式成立。
 
归纳假设
 
假设当n = k（k大于或等于1，k为整数）时，公式S = 2^k成立，即k根小棍有2^k种摆法。
 
归纳推理
 
当n = k + 1时，考虑新增加的这一根小棍。对于原来k根小棍的每一种摆法，新增加的这根小棍都有2种放置方式，要么与原来的小棍组合成新的摆法，要么单独作为一种新的摆法。所以k + 1根小棍的摆法种数是k根小棍摆法种数的2倍，即2*2^k = 2^{k + 1}种。
 
综上，由数学归纳法可知，对于任意正整数n，公式S = 2^n都成立。